Hyperfokální vzdálenost

Hyperfokální vzdálenost je velice zjednodušeně ostřící vzdálenost, kdy je ostré jak popředí, tak i nejvzdálenější objekty v pozadí snímku. V podstatě se nejedná o nic jiného, než o „extrémní“ aplikaci hloubky ostrosti. Hyperfokální vzdálenost je každopádně pojem, o kterém mluví řada fotografů, ale ne vždy jsou informace relevantní. Tímto článkem chci přinést trochu světla do této problematiky.

Hyperfokální vzdálenost – definice

K vysvětlení pojmu hyperfokální vzdálenost se používají dvě definice. Hyperfokální vzdálenost je…:

1. vzdálenost, od které se směrem do nekonečna bude jevit na snímku vše přijatelně ostré při zaostření na nekonečno.
2. vzdálenost, na kterou když se zaostří, bude na fotografii vše přijatelně ostré od poloviny této vzdálenosti do nekonečna.

Hyperfokální vzdálenost závisí na několika faktorech, a to na:

• ohniskové vzdálenosti objektivu,
• použité cloně objektivu,
• velikosti senzoru fotoaparátu,
• ale také na tom, co ještě považujete za ostré a co již nikoliv.

Co to tedy znamená? Předem to, že hyperfokální vzdálenost není nějaká přesně definovaná vzdálenost. Rozhodně na ni nelze spoléhat tak, že použijete několik „triků“ a vše bude najednou ostré. Vše sice záleží na hloubce ostrosti, ale toto pásmo hloubky ostrosti je vcelku dost pružné – podle podmínek.

Vzoreček hyperfokální vzdálenosti

Abyste zjistili hodnotu hyperfokální vzdálenosti, můžete využít vzoreček.

Hyperfokální vzdálenost [mm] = f ² / (F × c)

f: ohnisková vzdálenost objektivu [mm] (skutečná, nikoliv přepočítaná)
F: zvolené clonové číslo
c: rozptylový kroužek [mm]

Rozptylový kroužek

Každý z nás má trochu jinou představu o tom, co je a není ostré. Mladý zdravý člověk, bude mít jistě jiný zrak než 90letá osoba s několika dioptriemi. Aby ve věci bylo trochu více jasno, byl zaveden pojem rozptylový kroužek.

Představte si ve scéně malý světelný bod. Správně zaostřený obraz vytvoří na fotografii, resp. na senzoru fotoaparátu, také nepatrný světelný bod. Pokud není perfektně zaostřeno, zobrazí se na senzoru fotoaparátu menší či větší kruh. Průměr tohoto kruhu značí velikost rozostření obrazu. Právě tomuto kruhu se říká rozptylový kroužek, angl. Circle of Confusion (CoC).

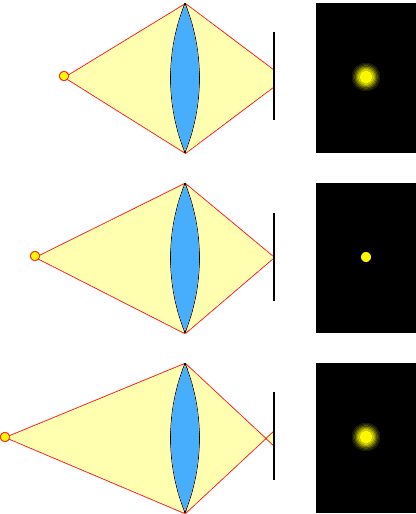
Zdravý člověk nedokáže rozeznat při běžné pozorovací („čtecí“) vzdálenosti objekty menší než přibližně 0,25 mm. Rozptylový kroužek proto na výsledné tištěné fotografii nesmí přesáhnout 0,25 mm. Kdyby přesáhl, jevil by se obraz jako rozmazaný.

Rozostření na senzoru

Kdybychom měli senzor fotoaparátu veliký jako list papíru (A4), nemusíme cokoliv přepočítávat. Tato velikost je dána historicky. Přesně se jedná o 8 × 12 palců, což přibližně odpovídá oné velikosti A4. Rozptylový kroužek na senzoru by v tomto případě odpovídal hodnotě 0,25 mm. Senzory fotoaparátů jsou ovšem mnohem menší. Proto se při přepočtu obraz ze senzoru zvětšuje na uvedenou velikost A4. Kolikrát je senzor fotoaparátu menší než A4, tolikrát se obraz zvětšuje. Při přepočtu se o stejnou hodnotu zmenšuje i rozptylový kroužek. Velikost rozptylového kroužku se proto mění s velikostí senzoru. Čím menší senzor, tím menší bude i rozptylový kroužek.

Pokud chcete určit hyperfokální vzdálenost, potřebujete správně určit velikost rozptylového kroužku. Pro příklad uvádím přehlednou tabulku s několika senzory.

Velikost senzoru	Rozptylový kroužek
A4 (hypoteticky)	0,25 mm
Full-frame	~ 0,03 mm
APS-C	~ 0,02 mm
4/3 systémy	~ 0,015 mm
1/2,5″	~ 0,005 mm

Hodnoty v tabulce jsou pouze přibližné. Velikost senzorů fotoaparátů se často uvádí ve velikostech ± 0,2 mm a tak se čísla vždy trochu liší. Není výjimečné se u APS-C Canonu setkat s více různými velikostmi senzorů (dle Wikipedie). Kupříkladu 22,2 × 14,8 mm (350D), 22,3 × 14,9 mm (50D), 22,4 × 15 mm (7D Mark II). Z toho plynou i různé výsledky.

Chcete-li vypočítat přesnou hodnotu rozptylového kroužku pro váš fotoaparát, zde je postup. Zjistěte si přesnou velikost senzoru fotoaparátu. Na základě rozměrů vypočítejte úhlopříčku senzoru. Vydělte velikost úhlopříčky A4 listu hodnotou úhlopříčky senzoru. Výsledkem vydělte číslo 0,25. Vyjde vám velikost rozptylového kroužku u vašeho fotoaparátu. Máte-li kupříkladu kompakt, půjde o dost malé číslo.

Hyperfokální vzdálenost teoreticky

Již víme vše potřebné a můžeme si hyperfokální vzdálenost snadno vypočítat. Nyní už stačí vyjít na focení s posuvným měřítkem, pokročilou kalkulačkou a měřícím pásmem (vtip).

Mohl bych teoreticky připravit tabulky pro hyperfokální vzdálenost všech nejpoužívanějších senzorů, základních clon a pro časté ohniskové vzdálenosti. Ve výsledku to znamená několik desítek tabulek, které jen zmatou čtenáře.

Místo toho vám nyní doporučím jednoduchou kalkulačku pro určení hyperfokální vzdálenosti:

• klasické webové rozhraní pro prohlížeče,
• mobilní verze,
• verze pro Android (prý v přípravě – červen 2018; nakonec nevydáno),
• verze pro iPhone / iPod.

Jak do tabulky zadávat

Otevřel jsem webové rozhraní kalkulačky. Rozhlédl se po pracovně a první fotoaparát, na kterém mi zůstal pohled, byl Canon EOS 5D Mark IV s „velkým“ full-frame senzorem. Hned vedle něj odpočíval objektiv Canon EF 14mm f/2,8 L II USM. Toto stačí a hurá na vyplnění tabulky.

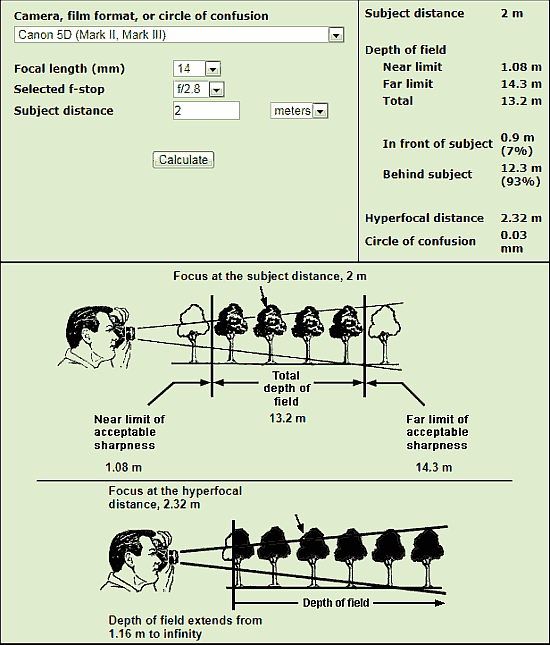
Nejprve z menu vyberu „Camera“, tedy fotoaparát. V tomto případě to bude volba Canon EOS 5D Mark II, III, které jsou mému fotoaparátu pravděpodobně nejblíže. Hodnota CoC na kalkulačce se shoduje i s mojí výše uvedenou tabulkou.

„Focal length (mm)“ značí ohniskovou vzdálenost objektivu. V mém případě je to oněch 14 mm. V části „Selected f-stop“ zadám hodnotu clony objektivu. Vyberu si rovnou dvě. První bude f/2,8. Druhá pak f/8. Následuje poslední položka „Subject distance“. Ta značí, jak daleko se nachází místo, na které ostřím. Není tu kolem mne moc místa, tak zvolím 2 metry. Nyní stačí kliknout na „Calculate“ a nechat si vše vypočítat.

Jak z tabulky číst

V pravé části tabulky se dozvídám, že hyperfokální vzdálenost (Hyperfocal distance) odpovídá 2,32 m. Ve spodní části tabulky (úplně dole) je pak další zajímavý související údaj. Pokud bych zaostřil přesně na hyperfokální vzdálenost, bylo by v obraze ostré vše od 1,16 m až do nekonečna. Hodnota 1,16 m je přesně polovina hyperfokální vzdálenosti. Já ale ostřil na vzdálenost menší než je hyperfokální vzdálenost.

Na obrázku výše se pak dozvídám, jak bude obraz přibližně vypadat v závislosti na výše zadaných parametrech. Tedy pokud ostřím na 2 m vzdálený objekt. Obraz by vypadal přibližně tak, že by bylo ostré vše ve vzdálenosti od 1 do 14 metrů od fotoaparátu. Vše blíže, nebo dále, by bylo již rozostřené.

Nyní změním hodnotu použité clony na dříve uvedených f/8. Rázem se hyperfokální vzdálenost zkrátila na 83 cm. Pokud bych s tímto nastavením ostřil na 2 metry vzdálený objekt, situace by se oproti předchozímu nastavení rapidně změnila. Obraz by byl ostrý přibližně již od 60 cm do nekonečna!

Test s Canon EOS 7D Mark II

Stejné nastavení jsem zopakoval pro zde často zmiňovaný fotoaparát Canon EOS 7D Mark II s menším senzorem. Jaký byl výsledek?

Hyperfokální vzdálenost u stejného objektivu při f/2,8 je cca 3,7 m. V případě clony f/8 se hyperfokální vzdálenost zkrátila na 1,3 metrů. Pokud bych pro druhý případ ostřil opět na 2 metry, obraz by byl ostrý od 80 cm do nekonečna. Jak je vidět, je to oproti full-frame senzoru jistý nemalý rozdíl.

Hyperfokální vzdálenost prakticky

Z kalkulačky výše plyne jedna nemilá věc. V některých případech prostě nejde dosáhnout toho, aby bylo popředí i nejvzdálenější pozadí maximálně zaostřené. Dokonce ani tehdy, pokud nastavíte na fotoaparátu, resp. objektivu, nejvyšší clonu. Pokud se s tím nesmíříte, máte v podstatě dvě možnosti:

• poodstoupit od fotografovaného objektu v popředí a snímat z větší vzdálenosti,
• udělat sérii fotografií, které postupně zaostříce na jiné místo a tyto fotografie poté „slepíte“ do jedné.

První varianta je často velmi snadná a dostupná. Jednoduše poodstoupíte a tím prodloužíte vzdálenost od fotoaparátu k fotografovanému objektu. V tu chvíli už se můžete dostat na hyperfokální vzdálenost, nebo do vzdálenosti delší (což ničemu nevadí).

Druhá varianta je vhodná zejména pro pokročilé fotografy. V podstatě na ní není mnoho těžkého. Pořídíte několik fotografií ze stativu a následně je správně prolnete. Nicméně tento článek se této technice nevěnuje. Podívejte se na článek o maskování a focus stackingu.

Hyperfokální vzdálenost prakticky (druhý test)

Není od věci si hyperfokální vzdálenost zkusit názorně a otestovat tak své objektivy. Pro tuto příležitost skvěle poslouží les / zahrada s několika prvky typu zahradní soška (prostě nejenom tráva).

Výše zobrazené scéna je v podstatě ideální prostor pro testování hyperfokální vzdálenosti (pro různé clony objektivu). Hlavně je dostupná prakticky komukoliv. Na scéně výše jsem se proto rozhodl otestovat kalkulačku hyperfokální vzdálenosti a objektiv samotný.

Níže můžete vidět výřez ze scény v různých vzdálenostech od fotografa při různých clonách objektivu. Ostřil jsem na nejbližší strom vpravo, který je vzdálený přibližně 3 metry od fotoaparátu. Ohnisková vzdálenost objektivu byla 17 mm. Fotilo se starým známým APS-C fotoaparátem Canon EOS 7D Mark II (má menší senzor než full-frame).

Konkrétní příklad hyperfokální vzdálenosti

Při výše uvedených údajích a cloně f/2,8 by měla být hyperfokální vzdálenost přibližně 5,4 metrů. Já ale ostřil pouze na 3 metry. To by dle kalkulačky znamená, že obraz by měl být ostrý přibližně od 2 metrů do necelých 7. Při pohledu na fotografii bych řekl, že tento údaj odpovídá. Cokoliv mimo cca 1,93 až 6,74 metrů od objektivu by mělo být rozmazané.

Při použité cloně f/4 je hyperfokální vzdálenost rovna 3,82 metrům. To je stále více než vzdálenost, na kterou ostřím. To mimo jiné znamená, že výše uvedený rozsah se v tomto případě prodlouží na 1,68 m až 13,9 metrů. Vzdálený strom (11,4 m) je ještě stále rozostřený (i když méně než v předchozím případě). V tomto případě za to částečně může jak scéna (resp. světelné podmínky), tak i částečně komprese JPEG souboru, ale také výřez 1:1. Kdybychom se na fotografii o velikosti A4 koukali z běžné vzdálenosti, bylo by to opět trochu jiné.

Při cloně f/9 je hyperfokální vzdálenost pouhých cca 1,7 metrů. Stále ostřím na stejné místo. Rozsah se opět trochu změnil – bližší hodnota je nyní cca 1,1 metrů, vzdálenější pak někde v nekonečnu. To znamená, že by prakticky vše na fotografii mělo být ostré. To fotografie splňuje.

Pro zajímavost přidávám ještě hodnotu clony f/22. Zde je již patrné rozostření obrazu vlivem difrakce obrazu (viz Wikipedia). To je také důvod, proč se nedoporučuje za každých okolností využívat zbytečně vysoká clonová čísla.

Osobní zkušenost

Někteří fotografové dělají z pojmu hyperfokální vzdálenost něco zbytečně složitého. Můj názor je ten, že stačí znát pouze své objektivy a vědět, jak se při různých ohniscích a nastavení clony chovají. Jenže k tomu je třeba trocha těch zkušeností a času stráveného focením (což v dnešní době není obvyklé).

Pokud (jako já) nechcete věc řešit za pomocí kalkulaček pro určení hyperfokální vzdálenosti, zde přikládám několik vlastních rad:

• otevřená (malá) clona → malá hloubka ostrosti (a opačně pro velkou clonu),
• jsou-li všechny hlavní objekty v jedné rovině → stačí nízká clona,
• je-li popředí blízké a pozadí vzdálené (více rovin) → vyšší clona,
• používám-li širokoúhlý objektiv → není obvykle třeba příliš clonit,
• u teleobjektivu → vysoká clona nebo velmi vzdálený objekt snímání zajistí ostré popředí i pozadí obrazu,
• focení na krátkou vzdálenost → malá hloubka ostrosti,
• přední hloubka ostrosti je vždy kratší než zadní hloubka ostrosti.

Těchto několik rad vám pomůže, aby vaše hlavní fotografované objekty byly korektně zaostřené. Nepotřebujete žádné „DoF kalkulačky“, nebo podobné věci. Nepotřebujete dokonce znát ani pojem hyperfokální vzdálenost. Je to jen o zkušenostech.

Hyperfokální vzdálenost v čajovně

V textu výše jsem psal, že existují případy, kdy nepomůže ani sebevětší clona objektivu. Ať se v tu chvíli snažíte sebevíc, obraz ostrý nebude. Připravil jsem si proto ukázkovou fotografii této dobroty.

Nápoj na fotografii výše se od mého fotoaparátu nacházel jen několik desítek centimetrů daleko. Abych ještě lépe demonstroval, že někdy nepomůže sebevětší clona, použil jsem u objektivu zoom. Ohnisková vzdálenost objektivu na fotografii níže je 55 mm, clona f/22.

Vysoké clony f/11 a více

Všimli jste si na ukázkové tabulce výše, jak difrakce obrazu negativně ovlivňuje ostrost snímku? Světlo procházející malou štěrbinou (vysoká clona) se chová tak trochu jako nějaký „prevít“. U objektivu může s rostoucí clonou docházet k difrakce obrazu, která dokáže snížit ostrost celé scény. To je však něco, čeho dosáhnout obvykle nepotřebujeme a nechceme. I s tím ale musíte při určování hyperfokální vzdálenosti počítat.

Mnoho návodů na internetu pod pojmy hyperfokální vzdálenost a ostrost celé scény, uvádí takový (ne)pěkný návod. „Zaostřete na výrazný objekt v popředí, nastavte maximální clonu a všechno budete mít ostré.“ Nebýt té difrakce obrazu, asi by se s tím dalo souhlasit. Vysoké clony navíc přináší ještě další nepříjemnosti. Pokud citelně zvýšíte pouze clonu, pravděpodobně tím docílíte značně tmavé fotografie. Aby byla fotografie expozičně správně, potřebujete zvýšit citlivost ISO, nebo prodloužit expoziční čas (příp. oboje). Oboje může opět negativně ovlivnit ostrost celého snímku.

Nyní již víte, že ne vždy potřebujete za každých okolností používat vysoké clony. Existují scény, kdy vám pro prokreslení celé scény stačí mnohem menší clona než ta maximální. Ale to už je buď na vaší osobní zkušenosti, nebo na tzv. DOF kalkulačkách.

Závěrem

Hyperfokální vzdálenost není nic složitého. Fotíte-li rádi krajiny, jistě brzy vypozorujete, jak se některé vaše objektivy chovají při různých nastaveních. Velice rychle si všimnete, že širokoúhlý objektiv bude mít obvykle velkou hloubku ostrosti. Naopak při focení s teleobjektivem na krátkou vzdálenost vám nepomůže sebevětší clona.

Fotíte-li opravdu precizně a snažíte-li se dosáhnout co nejvyšší ostrosti, pravděpodobně budete hyperfokální vzdálenost často využívat. V tomto případě zvažte vybavit své „chytré zařízení“ odpovídající aplikací pro určení hyperfokální vzdálenosti. Zažil jsem i moderního fotografa, který snímky přes Wi-Fi okamžitě po vyfotografování posílal do notebooku. Následně pak na 17″ obrazovce kontroloval, jestli jsou fotografie opravdu tak ostré, jak si vysnil.